Let There Be Light

时间限制：30s 空间限制：256MB

题目描述

假设三维空间里有一些光源和球型气球。光源可以视为点光源，它们都会向任何方向发射光线。气球表面可以吸收

光线并且不反射光线，令人惊讶的是在这个世界里气球可以重叠。你希望某个定点的总光照强度足够高。因此你需

要移走一些妨碍光线的气球。由于移除的成本问题，你能移走的气球数量是有限制的。因此你希望适当地移走一些

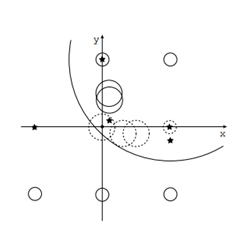
气球，从而最大化定点的总光照强度。下图给出了第一组样例的情况，由于所有的光源、气球中心和定点的 z 轴

坐标都是 0 ，所以下图显示的是 xy 平面。在图中，光源被表示成星星，气球被表示成圆。定点在原点，你可以

移走至多 4 个气球。对于这组数据，一种可能的方案是移走图中的虚线圆圈所对应的气球。

输入格式

输入包含多组测试数据。

每组数据的第一行包含三个正整数 N,M 和 R

其中 N 表示气球的数量（不超过2000），M表示光源的数量（不超过15）R表示可以移除的气球数量（不超过 N ）

接下来 N 行，每行四个整数，前三个整数表示一个气球中心的坐标，第四个整数表示这个气球的半径。

接下来 M 行，每行四个整数，前三个整数表示一个光源的坐标，第四个整数表示这个光源的亮度。

接下来一行包含三个整数，表示定点的坐标。

所有的坐标大于-500且小于500，半径大于0且小于500，光照强度大于0且小于80000。

对于定点，每个能照射到它的光源所能给它提供的光照强度等于光源的亮度除以二者的直线距离的平方，

而定点的光照强度就等于所有光源给它提供的光照强度之和。

你可以认为任意光源到定点的距离不小于1，且当任意气球的半径有小于0.01的误差时不会改变这个气球能否阻挡光源照射定点的状态。

输入以三个零作为结束。

输出格式

对于每组测试数据，输出一行包含一个实数表示最大的光照强度，

你的输出与答案的绝对误差不超过0.001时被认为是正确的。

样例输入

12 5 4
0 10 0 1
1 5 0 2
1 4 0 2
0 0 0 2
10 0 0 1
3 -1 0 2
5 -1 0 2
10 10 0 15
0 -10 0 1
10 -10 0 1
-10 -10 0 1
10 10 0 1
0 10 0 240
10 0 0 200
10 -2 0 52
-10 0 0 100
1 1 0 2
0 0 0
12 5 4
0 10 0 1
1 5 0 2
1 4 0 2
0 0 0 2
10 0 0 1
3 -1 0 2
5 -1 0 2
10 10 0 15
0 -10 0 1
10 -10 0 1
-10 -10 0 1
10 10 0 1
0 10 0 260
10 0 0 200
10 -2 0 52
-10 0 0 100
1 1 0 2
0 0 0
5 1 3
1 2 0 2
-1 8 -1 8
-2 -3 5 6
-2 1 3 3
-4 2 3 5
1 1 2 7
0 0 0
5 1 2
1 2 0 2
-1 8 -1 8
-2 -3 5 6
-2 1 3 3
-4 2 3 5
1 1 2 7
0 0 0
0 0 0

样例输出

3.5
3.6
1.1666666666666667
0.0

提示

没有写明提示

题目来源

鸣谢Tangjz提供试题