佛罗里达

时间限制：30s 空间限制：512MB

没有得到激光武器的苏联十分生气，他们决定派遣一支特种部队强行

登陆美国并造成一定的袭击。 Reddington 得到的情报是他们将在佛罗里达

海岸登陆，他决定派遣他的手下去阻击他们。可惜的是， Reddington 由于

不听从总统的意见，手中的部队只剩下了 N 个人。人与人之间会有一定的

矛盾值，第 i 个人与第 j 个人的矛盾值为 Ti,j，并且有 Ti,i = 0， Ti,j = Tj,i。

Reddington 希望将这 N 个人分为两支小分队，记为 A, B，每个人要么属

于分队 A 要么属于分队 B。对于一支小分队 S，其内部的不安值

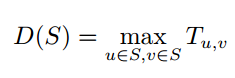
显然的，假如一支分队的不安值很高，那么作战能力就会很差。现在

给定你 N 以及一个 N ∗ N 的矩阵 T，你需要告诉 Reddington，最小的

D(A) + D(B) 是多少。

输入包括多组数据。

对于每组数据：

第一行一个整数 N。

接下来 N −1 行，第 i 行读入 N −i 个数，第 i 行第 j 个数表示 Ti,i+j。

2 ≤ N ≤ 250, 0 ≤ Ti,j ≤ 109，数据组数不超过 2 组

一行，最小的 D(A) + D(B) 是多少

4
//一种最优方案为： A = {1, 2, 4}, B = {3, 5}，此时 D(A) = 4, D(B) =0

没有写明提示

没有写明来源