[Balkan2009]year2012
时间限制:10s 空间限制:128MB
题目描述
传说2012-12-21是世界末日啊!(虽然今天已经是2012-12-26了……)人们都要逃亡了。到处都是自然灾害,导致地球上只有n个地方可以存活了。其中,我们在s号点,喜马拉雅山在t号点。对于这n个点,我们会用(Xi, Yi, Zi)来描述这些点,而坐标原点则是地球中心。显然,这n个地点是不会靠在一起的,那么我们必须要用飞机来飞行。已知我们所坐的飞机会保持一个恒定的速度v,并有一个容量为c的油箱。刚出发时,油箱是满的。而这n个点之中,不是能够两两之间互相飞行的。可以飞的航线只有m条,而每一条所需的油量都不一样(双向航线)。更糟糕的是,不是所有的点都能加油,那么就意味着飞行员每到一个地点,就不得不把油加满!已知两点之间的距离为坐标之间的球面距离(因为是在地球上嘛),而飞行总时间为(总距离/v),那么我们要从s号点飞到t号点至少需要多少时间呢?答案保留10位小数。
【数据范围及保证】
2<=n<=1000,整数,表示地点的数量。
1<=m<=10000,整数,表示可互相飞的航线数量。
1<=v<=1000,实数,精度最高为1e-3,表示飞机的恒定速度。
1<=c<=1000,整数,表示飞机油箱容量。
-100<= Xi, Yi, Zi<=100,实数,精度最高为1e-18,表示第i个点的坐标,其中数据保证Xi2+Yi2+Zi2(即地球半径)为一个恒定的正整数(尽管存在精度差,但是|精度差|<=1e-10,因此可认为每个点都严格在地球表面)。并保证,任意航线的长度>=1e-6.
1<=可加油的站点数量<=20
1<=地点的编号<=n; 1<=航线所需油量<=c
【注意事项】
1. 两点之间的距离为最短球面距离,可能有不止一条,但是只有一条有用。
2. a, b之间的航线可能中途经过c点,但这不代表a和c之间或b和c之间有航线。
3. 起飞,降落,加油等时间都可无视。
4. 若无解,则输出0.
5. 若|你输出的答案-标准答案|<=1e-4,则算正确。
输入格式
第1行四个正数n, m, v, c
接下来n行,每行四个数,Xi, Yi, Zi, Ri,其中Ri=1表示该点可加油,Ri=0表示该点不可加油。
接下来m行,每行3个正整数,Ak, Bk, Ck,其中Ak, Bk表示第k条航线所连接的两个站点。Ck表示该航线所需油量。
最后1行,两个正整数,s和t。
输出格式
仅一行,为所需最短时间。若无法到达t号点,则输出0.
样例输入
6 9 2.5 9 0.0 5.0 0.0 1 0.0 0.0 -5.0 0 0.0 -5.0 0.0 0 0.0 0.0 5.0 0 3.0 4.0 0.0 0 4.0 3.0 0.0 1 1 2 5 2 3 8 1 4 5 4 3 5 1 5 1 5 6 9 5 2 1 2 6 2 6 4 4 1 3
样例输出
12.5663706144
提示
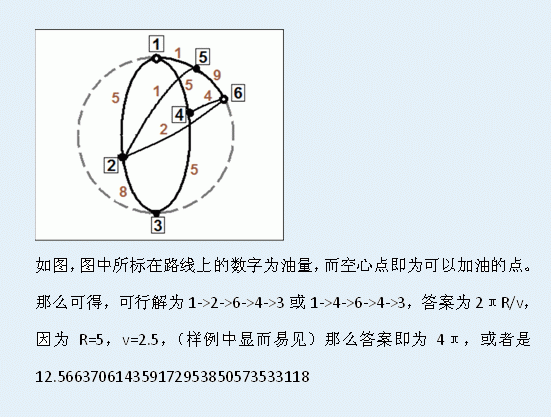
题目来源
没有写明来源